Jeśli uczyłeś się matematyki w szkole, to bez wątpienia nauczyłeś się reguły potęgowej określania pochodnej prostych funkcji. Jednak gdy funkcja zawiera pierwiastek kwadratowy lub znak pierwiastka kwadratowego, na przykład 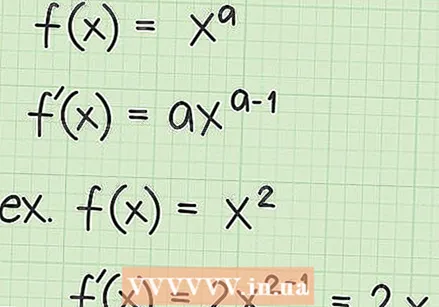${ displaystyle { sqrt {x}}}$Przejrzyj regułę potęgi dla instrumentów pochodnych. Pierwszą zasadą, której prawdopodobnie nauczyłeś się przy znajdowaniu pochodnych, jest reguła potęgi. Ta linia mówi, że dla zmiennej ${ displaystyle x}$Przepisz pierwiastek kwadratowy jako wykładnik. Aby znaleźć pochodną funkcji pierwiastka kwadratowego, pamiętaj, że pierwiastek kwadratowy z liczby lub zmiennej można również zapisać jako wykładnik. Termin pod znakiem korzenia jest zapisywany jako podstawa, podniesiona do potęgi 1/2. Termin jest również używany jako wykładnik pierwiastka kwadratowego. Spójrz na następujące przykłady:

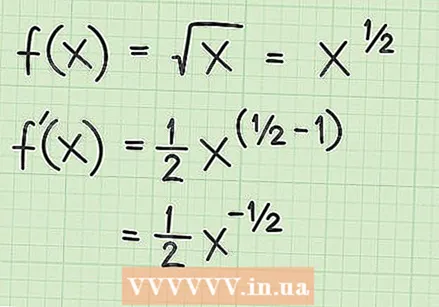• ${ Displaystyle { sqrt {x}} = x ^ { Frac {1} {2}}}$Zastosuj regułę mocy. Jeśli funkcja jest najprostszym pierwiastkiem kwadratowym, 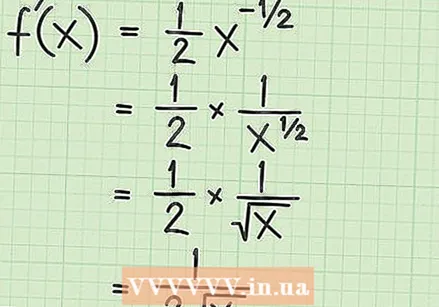${ displaystyle f (x) = { sqrt {x}}}$Uprość wynik. Na tym etapie powinieneś wiedzieć, że ujemny wykładnik oznacza odwrotność liczby z dodatnim wykładnikiem. Wykładnik 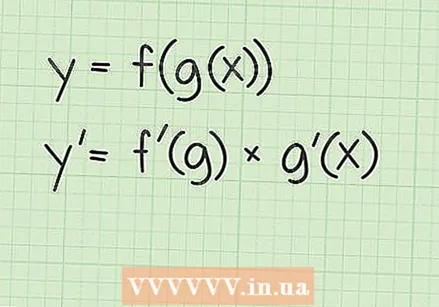${ displaystyle - { frac {1} {2}}}$Przejrzyj regułę łańcucha dla funkcji. Reguła łańcucha jest regułą dla pochodnych, której używasz, gdy oryginalna funkcja łączy funkcję w ramach innej funkcji. Reguła łańcucha mówi, że dla dwóch funkcji ${ displaystyle f (x)}$Zdefiniuj funkcje dla reguły łańcucha. Korzystanie z reguły łańcucha wymaga najpierw zdefiniowania dwóch funkcji, które składają się na funkcję połączoną. 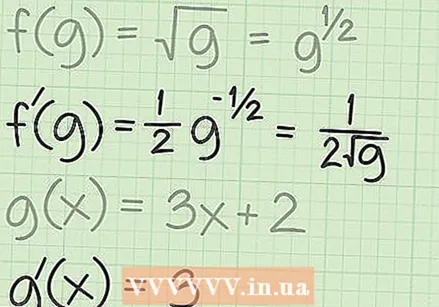W przypadku funkcji pierwiastka kwadratowego funkcją zewnętrzną jest ${ displaystyle f (g)}$Wyznacza pochodne dwóch funkcji. Aby zastosować regułę łańcucha do pierwiastka kwadratowego funkcji, musisz najpierw znaleźć pochodną ogólnej funkcji pierwiastka kwadratowego:
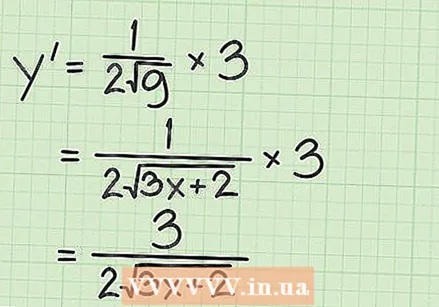  • ${ displaystyle f (g) = { sqrt {g}} = g ^ { frac {1} {2}}}$Połącz funkcje w regule łańcucha. Zasada łańcucha to ${ displaystyle y ^ { prime} = f ^ { prime} (g) * g ^ { prime} (x)}$Wyznacz pochodne funkcji pierwiastkowej przy użyciu szybkiej metody. Jeśli chcesz znaleźć pochodną pierwiastka kwadratowego zmiennej lub funkcji, możesz zastosować prostą regułę: pochodna zawsze będzie pochodną liczby znajdującej się poniżej pierwiastka kwadratowego podzielonej przez dwukrotność pierwotnego pierwiastka kwadratowego. Symbolicznie można to przedstawić jako:
    • Gdyby ${ displaystyle f (x) = { sqrt {u}}}$Znajdź pochodną liczby pod pierwiastkiem kwadratowym. Jest to liczba lub funkcja pod znakiem pierwiastka kwadratowego. Aby skorzystać z tej szybkiej metody, znajdź tylko pochodną liczby pod znakiem pierwiastka kwadratowego. Rozważ następujące przykłady:
      • W pozycji ${ displaystyle { sqrt {5x + 2}}}$Napisz pochodną pierwiastka kwadratowego jako licznik ułamka. Pochodna funkcji pierwiastkowej będzie zawierać ułamek. Licznik tego ułamka jest pochodną pierwiastka kwadratowego. Tak więc w powyższych przykładowych funkcjach pierwsza część pochodnej będzie wyglądać następująco:
        • Gdyby 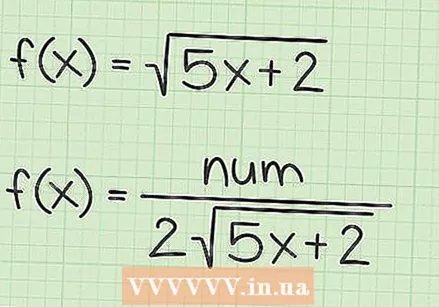${ displaystyle f (x) = { sqrt {5x + 2}}}$Napisz mianownik jako dwukrotność pierwotnego pierwiastka kwadratowego. Dzięki tej szybkiej metodzie mianownik jest dwukrotnością pierwotnej funkcji pierwiastka kwadratowego. Tak więc w trzech powyższych przykładowych funkcjach mianownikami pochodnych są:
          • Gdyby ${ displaystyle f (x) = { sqrt {5x + 2}}}$Połącz licznik i mianownik, aby znaleźć pochodną. Połóż razem dwie połówki ułamka, a wynik będzie pochodną pierwotnej funkcji.
            • Gdyby ${ displaystyle f (x) = { sqrt {5x + 2}}}$, niż ${ Displaystyle f ^ { prime} (x) = { Frac {5} {2 { sqrt {5x + 2}}}}}$
            • Gdyby ${ displaystyle f (x) = { sqrt {3x ^ {4}}}}$, niż ${ Displaystyle f ^ { prime} (x) = { Frac {12x ^ {3}} {2 { sqrt {3x ^ {4}}}}}}$
            • Gdyby ${ displaystyle f (x) = { sqrt { sin (x)}}}$, niż ${ Displaystyle f ^ { prime} (x) = { Frac { cos (x)} {2 { sqrt { sin (x)}}}}}$