Zawartość

• Kroki
• Rada

W przeciwieństwie do linii prostej współczynnik nachylenia (nachylenia) zmienia się w sposób ciągły, gdy porusza się ona wzdłuż krzywej. Analiza oferuje pomysł, że każdy punkt na wykresie można wyrazić jako współczynnik kąta lub „chwilową szybkość zmian”. Linia styczna w punkcie to prosta, która ma ten sam współczynnik kątowy i przechodzi przez ten sam punkt. Aby znaleźć równanie stycznej, musisz wiedzieć, jak wyprowadzić pierwotne równanie.

Kroki

Metoda 1 z 2: Znajdź równanie dla stycznej

1. 

   Funkcje wykresu i linie styczne (ten krok jest opcjonalny, ale zalecany). Tabela pomoże ci łatwiej zrozumieć problem i sprawdzić, czy odpowiedź jest rozsądna, czy nie. Narysuj wykresy funkcji na papierze siatkowym, w razie potrzeby użyj kalkulatora naukowego z funkcją wykresu. Narysuj linię styczną przechodzącą przez dany punkt (pamiętaj, że styczna przechodzi przez ten punkt i ma takie samo nachylenie jak znajdujący się tam wykres).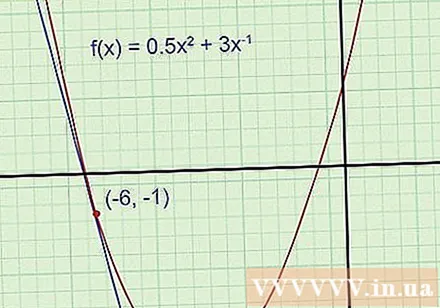
   • Przykład 1: Rysunek paraboliczny. Narysuj styczną przechodzącą przez punkt (-6, -1).
     Nawet jeśli nie znasz równania stycznej, nadal możesz zobaczyć, że jego nachylenie jest ujemne, a przecięcie jest ujemne (znacznie poniżej wierzchołka parabolicznego z rzędną -5,5). Jeśli ostateczna znaleziona odpowiedź nie jest zgodna z tymi szczegółami, w obliczeniach musi wystąpić błąd i należy sprawdzić ponownie.

2. 

   
   
   Uzyskaj pierwszą pochodną, ​​aby znaleźć równanie nachylenie stycznej. W przypadku funkcji f (x) pierwsza pochodna f '(x) przedstawia równanie nachylenia stycznej w dowolnym punkcie f (x). Istnieje wiele sposobów przyjmowania pochodnych. Oto prosty przykład wykorzystujący regułę mocy:
   • Przykład 1 (ciąg dalszy): Wykres jest określony funkcją.
     Przypominając regułę potęgi przy stosowaniu pochodnej:.
     Pierwsza pochodna funkcji = f '(x) = (2) (0,5) x + 3 - 0.
     f '(x) = x + 3. Zastępując x dowolną wartością a, równanie da nam nachylenie funkcji stycznej f (x) w punkcie x = a.

3. 

   
   
   Wprowadź wartość x rozważanego punktu. Przeczytaj problem, aby znaleźć współrzędne punktu, aby znaleźć styczną. Wprowadź współrzędne tego punktu w f '(x). Otrzymany wynik to nachylenie stycznej w powyższym punkcie.
   • Przykład 1 (ciąg dalszy): Punkt wspomniany w artykule to (-6, -1). Używając napięcia diagonalnego -6 do f '(x):
     f '(- 6) = -6 + 3 = -3
     Nachylenie stycznej wynosi -3.

4. 

   
   
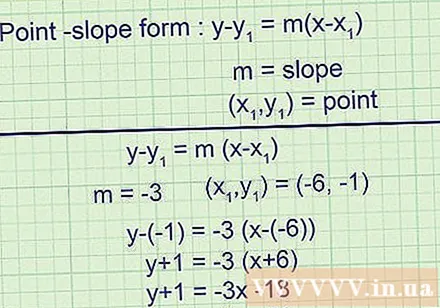
   Napisz równanie styczne w postaci linii prostej znającej współczynnik kąta i punkt na nim. To równanie liniowe jest zapisane jako. Wewnątrz, m jest nachyleniem i jest punktem na linii stycznej. Masz teraz wszystkie informacje potrzebne do napisania równania stycznego w tej formie.
   • Przykład 1 (ciąg dalszy):
     Nachylenie stycznej wynosi -3, więc:
     Styczna przechodzi przez punkt (-6, -1), więc końcowe równanie to:
     Krótko mówiąc, możemy:
     

5. 

   Graficzne potwierdzenie. Jeśli masz kalkulator graficzny, wykreśl oryginalną funkcję i styczną, aby sprawdzić, czy odpowiedź jest poprawna. Jeśli wykonujesz obliczenia na papierze, użyj wcześniej narysowanych wykresów, aby upewnić się, że w Twojej odpowiedzi nie ma oczywistych błędów.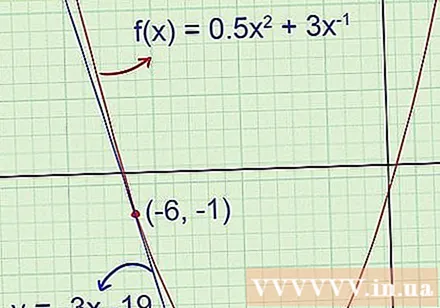
   • Przykład 1 (ciąg dalszy): Początkowy rysunek pokazuje, że styczna ma ujemne współczynniki kąta, a odsunięcie jest znacznie poniżej -5,5. Znalezione właśnie równanie stycznej to y = -3x -19, co oznacza, że ​​-3 to nachylenie kąta, a -19 to rzędna.

6. 

   Spróbuj rozwiązać trudniejszy problem. Ponownie wykonujemy wszystkie powyższe kroki.W tym momencie celem jest znalezienie stycznej w punkcie x = 2: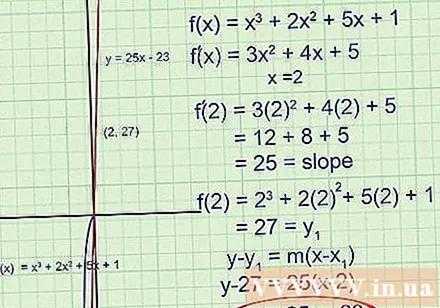
   • Znajdź pierwszą pochodną za pomocą reguły potęgi: Ta funkcja da nam nachylenie stycznej.
   • Dla x = 2 znajdź. To jest nachylenie przy x = 2.
   • Zauważ, że tym razem nie mamy punktu, a jedynie współrzędną x. Aby znaleźć współrzędną y, zamień x = 2 w oryginalnej funkcji :. Wynik to (2,27).
   • Napisz równanie na styczną przechodzącą przez punkt i mającą wyznaczony współczynnik kąta:
     
     W razie potrzeby zmniejsz do y = 25x - 23.
   Reklama

Metoda 2 z 2: Rozwiąż powiązane problemy

1. 

   Znajdź ekstremum na wykresie. Są to punkty, w których wykres zbliża się do lokalnego maksimum (punkt wyższy niż sąsiednie punkty po obu stronach) lub lokalnego minimum (niższego niż sąsiednie punkty po obu stronach). Styczna zawsze ma zerowy współczynnik w tych punktach (linia pozioma). Jednak współczynnik kąta nie wystarczy, aby stwierdzić, że jest to punkt skrajny. Oto jak je znaleźć: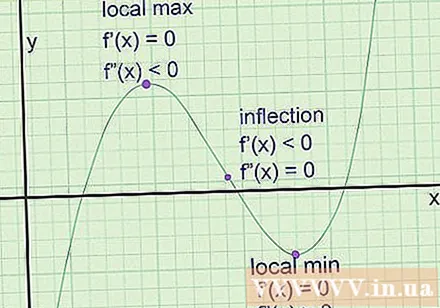
   • Weź pierwszą pochodną funkcji, aby otrzymać f '(x), nachylenie nachylenia stycznej.
   • Rozwiąż równanie f '(x) = 0, aby znaleźć punkt skrajny potencjał.
   • Biorąc pochodną kwadratową, aby otrzymać f '(x), równanie mówi nam o szybkości zmiany nachylenia stycznej.
   • Zmień współrzędne w każdym potencjalnym ekstremum za do f '' (x). Jeśli f '(a) jest dodatnie, mamy lokalne minimum na za. Jeśli f '(a) jest ujemne, mamy lokalny punkt maksymalny. Jeśli f '(a) wynosi 0, nie będzie to skrajność, jest to punkt przegięcia.
   • Jeśli osiągnięto maks. Lub min zaznajdź f (a), aby określić przecięcie.

2. 

   Znajdź równania normalnej. „Normalna” linia krzywej w danym punkcie przechodzi przez ten punkt i jest prostopadła do stycznej. Aby znaleźć równanie normalnej, użyj następującego wzoru: (nachylenie normalnej) (nachylenie normalnej) = -1, gdy mijają ten sam punkt na wykresie. Konkretnie: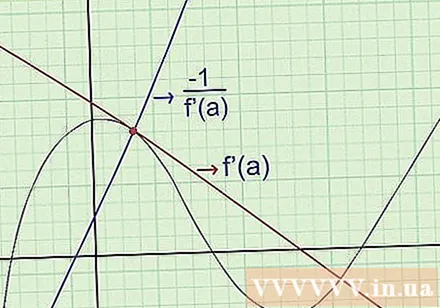
   • Znajdź f '(x), nachylenie stycznej.
   • Jeśli w danym punkcie mamy x = za: znajdź f '(a), aby określić nachylenie w tym punkcie.
   • Oblicz, aby znaleźć współczynnik normalnej.
   • Napisz równanie prostopadłej, aby poznać współczynniki kąta i punktu, przez który przechodzi.
   Reklama

Rada

• Jeśli to konieczne, przepisz oryginalne równanie w standardowej formie: f (x) = ... lub y = ...