Zawartość

• Kroki
• Rada

Prędkość definiuje się jako prędkość obiektu w danym kierunku. W wielu przypadkach, aby znaleźć prędkość, użyjemy równania v = s / t, gdzie v jest prędkością, s jest całkowitą odległością przemieszczenia się obiektu od jego pierwotnego położenia, at to czas potrzebny na przemieszczenie się obiektu. przejść całą drogę. Jednak w teorii ten wzór dotyczy tylko prędkości średni rzeczy w drodze. Obliczając prędkość obiektu w dowolnym momencie wzdłuż odległości. To jest Czas transportu i jest określone równaniem v = (ds) / (dt)lub innymi słowy, pochodna równania na średnią prędkość.

Kroki

Część 1 z 3: Oblicz prędkość chwilową

1. 

   
   
   Zacznij od równania służącego do obliczania prędkości na podstawie odległości przemieszczenia. Aby znaleźć prędkość chwilową, musimy najpierw mieć równanie, które wskazuje położenie obiektu (pod względem przemieszczenia) w dowolnym momencie. Oznacza to, że równanie musi mieć tylko jedną zmienną S po jednej stronie i obróć t Po drugiej stronie (niekoniecznie tylko jedna zmienna), na przykład:
   

   s = -1,5 t + 10 t + 4

   • W tym równaniu zmiennymi są:

     s = przemieszczenie. Odległość, na jaką obiekt przemieścił się z pierwotnego położenia. Na przykład, jeśli obiekt może przejść 10 metrów do przodu i 7 metrów do tyłu, jego całkowita odległość podróży wynosi 10 - 7 = 3 metry (nie 10 + 7 = 17m).

     t = czas. Ta zmienna jest prosta bez wyjaśnienia, zwykle mierzona w sekundach.

2. 

   
   
   Weź pochodną równania. Pochodna równania to kolejne równanie, które pokazuje nachylenie odległości w określonym czasie. Aby znaleźć pochodną równania na podstawie odległości przemieszczenia, weź różniczkę funkcji zgodnie z następującą ogólną zasadą, aby obliczyć pochodną: Jeśli y = a * x, pochodna = a * n * x. Dotyczy to wszystkich wyrażeń po stronie „t” równania.
   • Innymi słowy, zacznij robić różniczkę od lewej do prawej po stronie „t” równania. Za każdym razem, gdy napotkasz zmienną „t”, odejmujesz wykładnik przez 1 i mnożymy wyraz przez pierwotny wykładnik. Wszelkie stałe wyrazy (wyrazy bez „t”) znikną, ponieważ zostaną pomnożone przez 0. Proces w rzeczywistości nie jest tak trudny, jak mogłoby się wydawać - weźmy jako przykład równanie z powyższego kroku:
     

     s = -1,5 t + 10 t + 4
     (2) -1,5 t + (1) 10 t + (0) 4 t
     -3t + 10t
     -3t + 10

     
     

3. 

   Zamień „s” na „ds / dt”. Aby pokazać, że nowe równanie jest pochodną pierwotnego kwadratu, zastępujemy „s” symbolem „ds / dt”. Teoretycznie zapis ten jest „pochodną s na podstawie t”. Prostszy sposób na zrozumienie tego zapisu, ds / dt to nachylenie dowolnego punktu w początkowym równaniu. Na przykład, aby znaleźć nachylenie odległości opisanej równaniem s = -1,5t + 10t + 4 w czasie t = 5, podstawiamy „5” zamiast t w pochodnej równania.
   • W powyższym przykładzie pochodna równania wygląda następująco:
     

     ds / dt = -3t + 10

4. 

   Podstaw wartość t do nowego równania, aby znaleźć prędkość chwilową. Teraz, gdy mamy równanie pochodne, znalezienie prędkości chwilowej w dowolnym momencie jest bardzo łatwe. Wszystko, co musisz zrobić, to wybrać wartość t i zastąpić ją równaniem pochodnym. Na przykład, jeśli chcemy znaleźć prędkość chwilową przy t = 5, wystarczy podstawić „5” za t w równaniu pochodnym ds / dt = -3t + 10. Rozwiążemy równanie w następujący sposób:
   

   ds / dt = -3t + 10
   ds / dt = -3 (5) + 10
   ds / dt = -15 + 10 = -5 metrów / sekundę

   • Zwróć uwagę, że powyżej używamy jednostki „metry / sekundę”.Ponieważ rozwiązujemy problem z przemieszczeniem w metrach i czasem w sekundach, gdzie prędkość jest dokładnie przemieszczeniem w czasie, ta jednostka jest odpowiednia.
   Reklama

Część 2 z 3: Graficzne szacowanie prędkości chwilowej

1. 

   Wykres odległości ruchu obiektu w czasie. W powyższej sekcji powiedzieliśmy, że pochodna jest również formułą, która pozwala nam znaleźć nachylenie w dowolnym punkcie równania wziętego z pochodnej. W rzeczywistości, jeśli pokażesz odległość poruszania się obiektu na wykresie, Nachylenie wykresu w dowolnym punkcie to chwilowa prędkość obiektu w tym punkcie.
   • Aby wykreślić odległości ruchu, użyj osi X dla czasu i osi Y dla przemieszczenia. Następnie określasz liczbę punktów, wstawiając wartości t do równania ruchu, wynikiem jest s wartości i kropkujesz punkty t, s (x, y) na wykresie.
   • Zauważ, że wykres może rozciągać się poniżej osi X. Jeśli linia pokazująca ruch obiektu schodzi w dół osi X, oznacza to, że obiekt porusza się do tyłu ze swojej pierwotnej pozycji. Ogólnie wykres nie będzie wychodził poza oś Y - zwykle nie mierzymy prędkości obiektów cofających się w czasie!

2. 

   Wybierz punkt P i punkt Q znajdujący się w pobliżu punktu P na wykresie. Aby znaleźć nachylenie wykresu w punkcie P, używamy techniki „znajdowania granic”. Znalezienie granicy oznacza wzięcie dwóch punktów (P i Q (jeden punkt w pobliżu P)) na krzywej i znalezienie nachylenia linii łączącej te dwa punkty, powtarzając ten proces w miarę zmniejszania się odległości między P i Q. stopniowo.
   • Załóżmy, że odległość przesunięcia ma punkty (1; 3) i (4; 7). W tym przypadku, jeśli chcemy znaleźć nachylenie w (1; 3), możemy ustawić (1; 3) = P i (4; 7) = Q.

3. 

   Znajdź nachylenie między P i Q. Nachylenie między P i Q jest różnicą wartości y dla P i Q w stosunku do różnicy wartości x dla P i Q. Innymi słowy, H = (y_Q - y_P.) / (x_Q - x_P.), gdzie H to nachylenie między dwoma punktami. W tym przykładzie nachylenie między P i Q wynosi:
   

   H = (y_Q - y_P.) / (x_Q - x_P.)
   H = (7 - 3) / (4 - 1)
   H = (4) / (3) = 1,33

4. 

   Powtórz kilka razy, przesuwając Q bliżej P. Celem jest zmniejszenie odległości między P i Q, aż osiągną jeden punkt. Im mniejsza odległość między P i Q, tym nachylenie tego nieskończenie małego odcinka będzie bliżej nachylenia w punkcie P. Powtórz kilka razy dla naszego przykładowego równania, używając punktów (2; 4 , 8), (1,5; 3,95) i (1,25; 3,49) dają Q, a początkowe współrzędne P to (1; 3):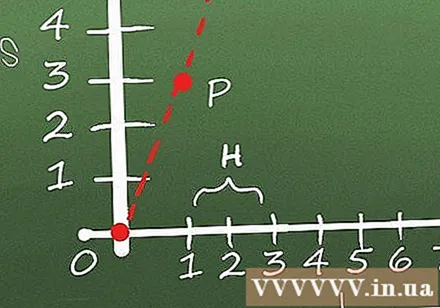
   

   Q = (2; 4,8): H = (4,8 - 3) / (2 - 1)
   H = (1,8) / (1) = 1,8
   
   Q = (1,5; 3,95): H = (3,95 - 3) / (1,5 - 1)
   H = (0,95) / (0,5) = 1,9
   
   Q = (1,25; 3,49): H = (3,49 - 3) / (1,25 - 1)
   H = (0,49) / (0,25) = 1,96

5. 

   Szacuje nachylenie bardzo małego segmentu na krzywej wykresu. Gdy Q zbliża się coraz bardziej do P, H będzie stopniowo zbliżać się do nachylenia w P. Wreszcie, na bardzo małej linii, H będzie nachyleniem w P. Ponieważ nie możemy zmierzyć ani obliczyć Długość linii jest bardzo mała, więc należy oszacować nachylenie w punkcie P tylko wtedy, gdy jest ono wyraźnie widoczne z obliczanych przez nas punktów.
   • W powyższym przykładzie, gdy przybliżamy H do P, otrzymujemy wartości H równe 1,8; 1,9 i 1,96. Ponieważ liczby te zbliżają się do 2, możemy powiedzieć 2 jest przybliżoną wartością nachylenia przy P.
   • Pamiętaj, że nachylenie w dowolnym punkcie wykresu jest pochodną równania wykresu w tym punkcie. Ponieważ wykres przedstawia przemieszczenie obiektu w czasie, jak widzieliśmy w poprzedniej sekcji, jego chwilowa prędkość w dowolnym punkcie jest pochodną odległości przemieszczenia obiektu w punkcie problemowym. Dostęp, możemy powiedzieć 2 metry / sek jest przybliżoną oceną prędkości chwilowej, gdy t = 1.
   Reklama

Część 3 z 3: Przykładowy problem

1. 

   Znajdź prędkość chwilową, gdy t = 1, z równaniem przemieszczenia s = 5t - 3t + 2t + 9. Podobnie jak w przykładzie w pierwszej sekcji, ale jest to sześcienny zamiast kwadratowy, więc możemy rozwiązać problem w ten sam sposób.
   • Najpierw weź pochodną równania:
     

     s = 5t - 3t + 2t + 9
     s = (3) 5t - (2) 3t + (1) 2t
     15t - 6t + 2t - 6t + 2

   • Następnie zamieniamy wartość t (4) na:
     

     s = 15 t - 6 t + 2
     15(4) - 6(4) + 2
     15(16) - 6(4) + 2
     240 - 24 + 2 = 22 metry na sekundę

2. 

   Użyj metody estymacji grafowej, aby znaleźć chwilową prędkość w (1; 3) dla równania przemieszczenia s = 4t - t. W tym zadaniu używamy współrzędnych (1; 3) jako punktu P, ale musimy znaleźć inne punkty Q znajdujące się w pobliżu. Następnie wszystko, co musimy zrobić, to znaleźć wartości H i wydedukować wartość szacowaną.
   • Najpierw znajdujemy punkty Q, gdy t = 2; 1,5; 1.1 i 1.01.
     

     s = 4t - t
     
     t = 2: s = 4 (2) - (2)
     4 (4) - 2 = 16 - 2 = 14, więc Q = (2; 14)
     
     t = 1,5: s = 4 (1,5) - (1,5)
     4 (2,25) - 1,5 = 9 - 1,5 = 7,5, a więc Q = (1,5; 7,5)
     
     t = 1,1: s = 4 (1,1) - (1,1)
     4 (1,21) - 1,1 = 4,84 - 1,1 = 3,74, a więc Q = (1, 1; 3,74)
     
     t = 1,01: s = 4 (1,01) - (1,01)
     4 (10201) - 1,01 = 4,0804 - 1,01 = 3,0704, więc to wszystko Q = (1,01; 3,0704)

   • Następnie otrzymamy wartości H:
     

     Q = (2; 14): H = (14 - 3) / (2 - 1)
     H = (11) / (1) = 11
     
     Q = (1,5; 7,5): H = (7,5 - 3) / (1,5 - 1)
     H = (4,5) / (0,5) = 9
     
     Q = (1, 1; 3,74): H = (3,74 - 3) / (1,1 - 1)
     H = (0,74) / (0,1) = 7,3
     
     Q = (1,01; 3,0704): H = (3,0704 - 3) / (1,01 - 1)
     H = (0,0704) / (0,01) = 7,04

   • Ponieważ wartości H wydają się być bliższe 7, możemy tak powiedzieć 7 metrów na sekundę jest przybliżonym oszacowaniem prędkości chwilowej o współrzędnej (1; 3).
   Reklama

Rada

• Aby znaleźć przyspieszenie (zmianę prędkości w czasie), użyj metody z części pierwszej, aby uzyskać pochodną równania przemieszczenia. Następnie weź pochodną ponownie do znalezionego przed chwilą równania pochodnego. W rezultacie masz równanie na przyspieszenie w danym momencie - wszystko, co musisz zrobić, to podłączyć w czasie.
• Równanie pokazujące zależność między Y (odległość przemieszczenia) i X (czas) może być bardzo proste, np. Y = 6x + 3. W tym przypadku nachylenie jest stałe i nie trzeba brać pochodna do obliczenia nachylenia, to znaczy wynika z podstawowego równania Y = mx + b dla wykresu liniowego, tj. nachylenie wynosi 6.
• Odległość przemieszczenia jest podobna do odległości, ale ma kierunek, więc jest wielkością wektorową, a prędkość jest wielkością skalarną. Odległości podróży mogą być ujemne, podczas gdy odległości mogą być tylko dodatnie.