Zawartość

• Kroki
• Porady

Funkcja wymierna ma postać y = N (x) / D (x), gdzie N i D są wielomianami. Aby dokładnie wykreślić taką funkcję, potrzebna jest dobra znajomość algebry, w tym obliczeń różniczkowych. Rozważmy następujący przykład: tak = (2x - 6x + 5)/(4x + 2).

Kroki

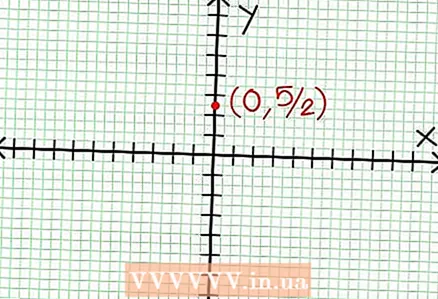1. 1 Znajdź punkt przecięcia y wykresu. Aby to zrobić, wstaw do funkcji x = 0 i otrzymaj y = 5/2. Zatem punkt przecięcia wykresu z osią Y ma współrzędne (0, 5/2).Umieść ten punkt na płaszczyźnie współrzędnych.
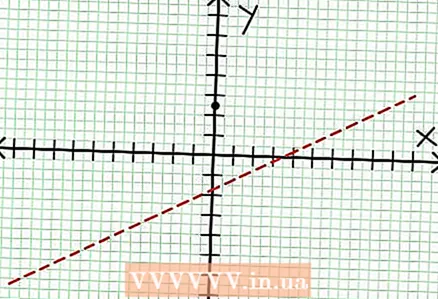2. 2 Znajdź poziome asymptoty. Podziel licznik przez mianownik (w kolumnie), aby określić zachowanie „y” przy wartościach „x” dążących do nieskończoności. W naszym przykładzie podział będzie następujący: tak = (1/2)x - (7/4) + 17/(8x + 4). Dla dużych wartości dodatnich lub ujemnych „x” 17 / (8x + 4) dąży do zera, a wykres zbliża się do linii prostej podanej przez funkcję tak = (1/2)x - (7/4). Używając kropkowanej linii, wykreśl tę funkcję.
   • Jeżeli stopień licznika jest mniejszy niż stopień mianownika, to nie można podzielić licznika przez mianownik, a asymptota zostanie opisana funkcją w = 0.
   • Jeżeli stopień licznika jest równy stopniowi mianownika, to asymptota jest linią poziomą równą stosunkowi współczynników przy „x” w najwyższym stopniu.
   • Jeżeli stopień licznika jest o 1 większy niż stopień mianownika, to asymptotą jest nachylona linia prosta, której nachylenie jest równe stosunkowi współczynników przy „x” do najwyższego stopnia.
   • Jeżeli stopień licznika jest większy niż stopień mianownika o 2, 3 itd., to dla dużych wartości |NS| oznaczający w mają tendencję do nieskończoności (dodatniej lub ujemnej) w postaci kwadratu, sześcianu lub innego stopnia wielomianu. W takim przypadku najprawdopodobniej nie trzeba budować dokładnego wykresu funkcji uzyskanej przez podzielenie licznika przez mianownik.
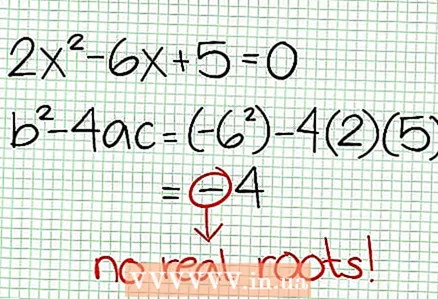3. 3 Znajdź zera funkcji. Funkcja wymierna ma zera, gdy jej licznik wynosi zero, czyli N (NS) = 0. W naszym przykładzie 2x - 6x + 5 = 0. Wyróżnik tego równania kwadratowego: b - 4AC = 6 - 4 * 2 * 5 = 36 - 40 = -4. Ponieważ wyróżnik jest ujemny, to N (NS), a więc F (NS) nie ma prawdziwych korzeni. Wykres funkcji wymiernej nie przecina osi X. Jeśli funkcja ma zera (pierwiastki), umieść je na płaszczyźnie współrzędnych.
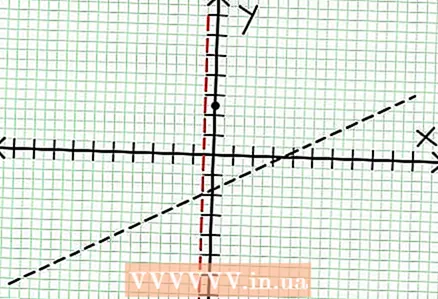4. 4 Znajdź pionowe asymptoty. Aby to zrobić, ustaw mianownik na zero. W naszym przykładzie 4x + 2 = 0 i NS = -1/2. Wykreśl pionową asymptotę za pomocą linii kropkowanej. Jeśli za jakąś wartość NS N (NS) = 0 i D (NS) = 0, to asymptota pionowa albo istnieje, albo nie istnieje (jest to rzadki przypadek, ale lepiej o tym pamiętać).
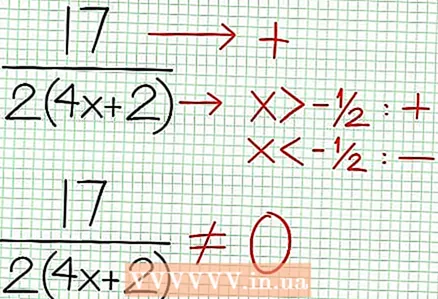5. 5 Spójrz na resztę licznika podzieloną przez mianownik. Czy jest dodatnia, ujemna czy zerowa? W naszym przykładzie reszta to 17, co jest wartością dodatnią. Mianownik 4x + 2 dodatnie na prawo od pionowej asymptoty i ujemne na lewo od niej. Oznacza to, że wykres funkcji wymiernej dla dużych wartości dodatnich NS zbliża się do asymptoty z góry, a dla dużych wartości ujemnych NS - od dołu. Od 17 / (8x + 4) nigdy nie jest równy zero, to wykres tej funkcji nigdy nie przetnie prostej określonej przez funkcję w = (1/2)NS - (7/4).
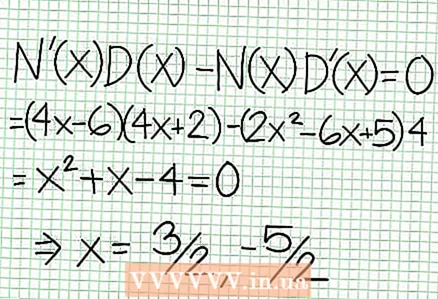6. 6 Znajdź lokalne ekstrema. Ekstremum lokalne istnieje dla N '(x) D (x) - N (x) D '(x) = 0. W naszym przykładzie N ’(x) = 4x - 6 i D '(x) = 4. N ’(x) D (x) - N (x) D '(x) = (4x - 6)(4x + 2) - (2x - 6x + 5)*4 = x + x - 4 = 0. Rozwiązując to równanie, stwierdzasz, że x = 3/2 i x = -5/2. (Nie są to w pełni dokładne wartości, ale są odpowiednie w naszym przypadku, gdy superprecyzja nie jest potrzebna.)
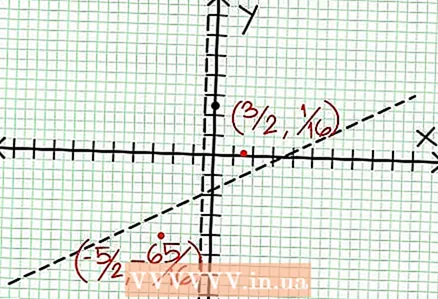7. 7 Znajdź wartość w dla każdego ekstremum lokalnego. Aby to zrobić, zastąp wartości NS do pierwotnej funkcji wymiernej. W naszym przykładzie f (3/2) = 1/16 i f (-5/2) = -65/16. Odłóż na bok punkty (3/2, 1/16) i (-5/2, -65/16) na płaszczyźnie współrzędnych. Ponieważ obliczenia opierają się na przybliżonych wartościach (z poprzedniego kroku), znalezione minimum i maksimum również nie są do końca dokładne (ale prawdopodobnie bardzo zbliżone do dokładnych wartości). (Punkt (3/2, 1/16) jest bardzo zbliżony do lokalnego minimum. Począwszy od kroku 3 wiemy, że w zawsze pozytywne dla NS> -1/2 i znaleźliśmy małą wartość (1/16); w związku z tym wartość błędu jest w tym przypadku bardzo mała).
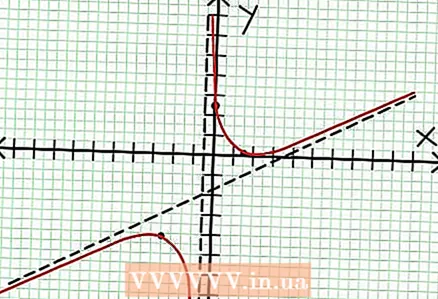8. 8 Połącz punkty oczekujące i płynnie rozciągnij wykres do asymptot (nie zapomnij o prawidłowym kierunku zbliżania się wykresu do asymptot). Pamiętaj, że wykres nie może przecinać osi X (patrz krok 3). Wykres również nie przecina się z asymptotami poziomymi i pionowymi (patrz krok 5). Nie zmieniaj kierunku wykresu z wyjątkiem skrajnych punktów znalezionych w poprzednim kroku.

Porady

• Jeśli wykonałeś powyższe kroki ściśle w kolejności, nie ma potrzeby obliczania drugich pochodnych (lub podobnych wielkości złożonych), aby przetestować swoje rozwiązanie.
• Jeśli nie musisz obliczać wartości wielkości, możesz zastąpić znajdowanie ekstremów lokalnych, obliczając dodatkowe pary współrzędnych (NS, w) między każdą parą asymptot. Co więcej, jeśli nie obchodzi Cię, jak działa opisana metoda, nie zdziw się, dlaczego nie możesz znaleźć pochodnej i rozwiązać równania N '(x) D (x) - N (x) D '(x) = 0.
• W niektórych przypadkach będziesz musiał pracować z wielomianami wyższego rzędu. Jeśli nie możesz znaleźć dokładnego rozwiązania za pomocą faktoryzacji, formuł itp., oszacuj możliwe rozwiązania za pomocą metod numerycznych, takich jak metoda Newtona.
• W rzadkich przypadkach licznik i mianownik mają wspólny czynnik zmienny. Zgodnie z opisanymi krokami doprowadzi to do zera i pionowej asymptoty w tym samym miejscu. Nie jest to jednak możliwe, a wyjaśnienie jest jednym z następujących:
  • Zero w N (NS) ma większą krotność niż zero w D (NS). Wykres F (NS) dąży do zera w tym momencie, ale nie jest tam zdefiniowany. Wskaż to, rysując okrąg wokół punktu.
  • Zero w N (NS) i zero w D (NS) mają taką samą wielokrotność. Wykres zbliża się do pewnego punktu niezerowego przy tej wartości NSale nie są tam zdefiniowane. Wskaż to, rysując okrąg wokół punktu.
  • Zero w N (NS) ma mniejszą krotność niż zero w D (NS). Jest tu pionowa asymptota.