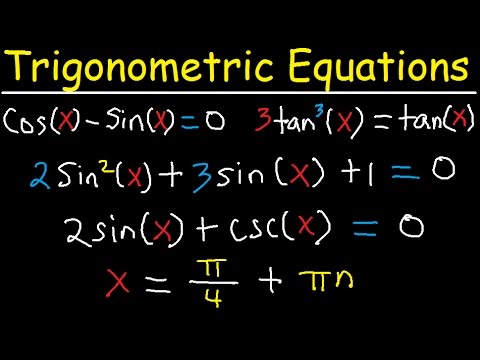
Zawartość

• Do kroku

Równanie trygonometryczne to równanie zawierające jedną lub więcej funkcji trygonometrycznych zmiennej krzywej trygonometrycznej x. Rozwiązanie dla x oznacza znalezienie wartości krzywych trygonometrycznych, których funkcje trygonometryczne powodują, że równanie trygonometryczne jest prawdziwe.

• Odpowiedzi lub wartości krzywych rozwiązania są wyrażane w stopniach lub radianach. Przykłady:

x = Pi / 3; x = 5Pi / 6; x = 3Pi / 2; x = 45 stopni; x = 37,12 stopnia; x = 178,37 stopnia

• Uwaga: Na okręgu jednostkowym funkcje trygonometryczne dowolnej krzywej są równe funkcjom trygonometrycznym odpowiedniego kąta. Okrąg jednostkowy definiuje wszystkie funkcje trygonometryczne zmiennej krzywej x. Jest również używany jako dowód przy rozwiązywaniu podstawowych równań i nierówności trygonometrycznych.
• Przykłady równań trygonometrycznych:
  • sin x + sin 2x = 1/2; tan x + łóżeczko x = 1,732;
  • cos 3x + sin 2x = cos x; 2sin 2x + cos x = 1.

1. Koło jednostkowe.
   • To jest okrąg o promieniu = 1, gdzie O jest początkiem. Okrąg jednostkowy definiuje 4 główne funkcje trygonometryczne zmiennej krzywej x, która okrąża ją w kierunku przeciwnym do ruchu wskazówek zegara.
   • Kiedy krzywa o wartości x zmienia się na okręgu jednostkowym, to trzyma:
   • Oś pozioma OAx definiuje funkcję trygonometryczną f (x) = cos x.
   • Oś pionowa OBy definiuje funkcję trygonometryczną f (x) = sin x.
   • Oś pionowa AT określa funkcję trygonometryczną f (x) = tan x.
   • Oś pozioma BU definiuje funkcję trygonometryczną f (x) = cot x.

• Okrąg jednostkowy służy również do rozwiązywania podstawowych równań trygonometrycznych i standardowych nierówności trygonometrycznych, biorąc pod uwagę różne położenia krzywej x na okręgu.

Do kroku

1. Zrozum metodę rozwiązania.
   • Aby rozwiązać równanie trygonometryczne, należy je przekształcić w jedno lub więcej podstawowych równań trygonometrycznych. Rozwiązanie równań trygonometrycznych ostatecznie prowadzi do rozwiązania 4 podstawowych równań trygonometrycznych.
2. Umiejętność rozwiązywania podstawowych równań trygonometrycznych.
   • Istnieją 4 podstawowe równania trygonometryczne:
   • sin x = a; cos x = a
   • tan x = a; łóżeczko x = a
   • Możesz rozwiązać podstawowe równania trygonometryczne, badając różne pozycje krzywej x na okręgu trygonometrycznym i używając tabeli konwersji trygonometrycznej (lub kalkulatora). Aby w pełni zrozumieć, jak rozwiązać te i podobne podstawowe równania trygonometryczne, przeczytaj następującą książkę: „Trygonometria: Rozwiązywanie równań trygonometrycznych i nierówności” (Amazon E-book 2010).
   • Przykład 1. Wyznacz sin x = 0,866. Tabela konwersji (lub kalkulator) daje odpowiedź: x = Pi / 3. Koło trygonometryczne daje inną krzywą (2Pi / 3) o tej samej wartości dla sinusa (0,866). Okrąg trygonometryczny zapewnia również nieskończoną liczbę odpowiedzi zwanych odpowiedziami rozszerzonymi.
   • x1 = Pi / 3 + 2k.Pi, a x2 = 2Pi / 3. (Odpowiedzi w okresie (0, 2Pi))
   • x1 = Pi / 3 + 2k Pi, a x2 = 2Pi / 3 + 2k Pi. (Szczegółowe odpowiedzi).
   • Przykład 2. Rozwiąż: cos x = -1/2. Kalkulatory dają x = 2 Pi / 3. Okrąg trygonometryczny również daje x = -2Pi / 3.
   • x1 = 2Pi / 3 + 2k.Pi, a x2 = - 2Pi / 3. (Odpowiedzi na okres (0, 2Pi))
   • x1 = 2Pi / 3 + 2k Pi, a x2 = -2Pi / 3 + 2k.Pi. (Rozszerzone odpowiedzi)
   • Przykład 3. Rozwiąż: tan (x - Pi / 4) = 0.
   • x = Pi / 4; (Odpowiedź)
   • x = Pi / 4 + k Pi; (Rozszerzona odpowiedź)
   • Przykład 4. Rozwiąż: łóżeczko 2x = 1,732. Kalkulatory i koło trygonometryczne dają:
   • x = Pi / 12; (Odpowiedź)
   • x = Pi / 12 + k Pi; (Rozszerzone odpowiedzi)
3. Poznaj transformacje stosowane przy rozwiązywaniu równań trygonometrycznych.
   • Aby przekonwertować dane równanie trygonometryczne na standardowe równania trygonometryczne, użyj standardowych konwersji algebraicznych (faktoryzacja, współczynnik wspólny, wielomiany ...), definicji i właściwości funkcji trygonometrycznych i tożsamości trygonometrycznych. Jest ich około 31, 14 z nich to tożsamości trygonometryczne, od 19 do 31, zwane również tożsamościami transformacji, ponieważ są one używane do konwersji równań trygonometrycznych. Zobacz powyższą książkę.
   • Przykład 5: Równanie trygonometryczne: sin x + sin 2x + sin 3x = 0 można przekształcić w iloczyn podstawowych równań trygonometrycznych przy użyciu tożsamości trygonometrycznych: 4cos x * sin (3x / 2) * cos (x / 2) = 0. Podstawowe równania trygonometryczne do rozwiązania to: cos x = 0; sin (3x / 2) = 0; i cos (x / 2) = 0.
4. Znajdź krzywe, dla których znane są funkcje trygonometryczne.
   • Zanim nauczysz się rozwiązywać równania trygonometryczne, musisz wiedzieć, jak szybko znaleźć krzywe, dla których znane są funkcje trygonometryczne. Wartości przeliczeniowe krzywych (lub kątów) można określić za pomocą tabel trygonometrycznych lub kalkulatora.
   • Przykład: wyznacz cos x = 0,732. Kalkulator podaje rozwiązanie x = 42,95 stopnia. Okrąg jednostkowy daje inne krzywe o tej samej wartości cosinusa.
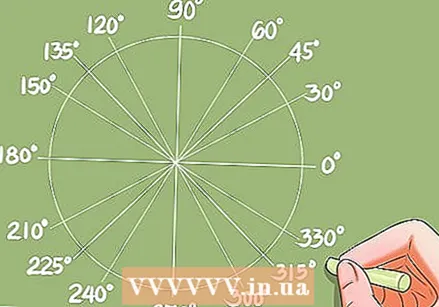
5. Narysuj łuk odpowiedzi na okręgu jednostkowym.
   • Możesz utworzyć wykres ilustrujący rozwiązanie na okręgu jednostkowym. Punktami końcowymi tych krzywych są regularne wielokąty na okręgu trygonometrycznym. Kilka przykładów:
   • Punkty końcowe krzywej x = Pi / 3 + k. Pi / 2 to kwadrat na okręgu jednostkowym.
   • Krzywe x = Pi / 4 + k.Pi / 3 są reprezentowane przez współrzędne sześciokąta na okręgu jednostkowym.
6. Dowiedz się, jak rozwiązywać równania trygonometryczne.
   • Jeśli dane równanie trygonometryczne zawiera tylko jedną funkcję trygonometryczną, rozwiąż je jako standardowe równanie trygonometryczne. Jeśli dane równanie zawiera dwie lub więcej funkcji trygonometrycznych, istnieją 2 metody rozwiązania, w zależności od opcji konwersji równania.
     • A. Metoda 1.
   • Zamień równanie trygonometryczne na iloczyn postaci: f (x). G (x) = 0 lub f (x). G (x). H (x) = 0, gdzie f (x), g (x) a h (x) to podstawowe równania trygonometryczne.
   • Przykład 6. Rozwiąż: 2cos x + sin 2x = 0. (0 x 2Pi)
   • Rozwiązanie. Zastąp sin 2x w równaniu, używając tożsamości: sin 2x = 2 * sin x * cos x.
   • cos x + 2 * sin x * cos x = 2cos x * (sin x + 1) = 0. Następnie rozwiąż 2 standardowe funkcje trygonometryczne: cos x = 0 i (sin x + 1) = 0.
   • Przykład 7. Rozwiąż: cos x + cos 2x + cos 3x = 0 (0 x 2Pi)
   • Rozwiązanie: Zamień to na iloczyn, używając tożsamości trygonometrycznych: cos 2x (2 cos x + 1) = 0. Teraz rozwiąż 2 podstawowe równania trygonometryczne: cos 2x = 0 i (2 cos x + 1) = 0.
   • Przykład 8. Rozwiąż: sin x - sin 3x = cos 2x. (0 x 2Pi)
   • Rozwiązanie: Przekształć to w iloczyn, używając tożsamości trygonometrycznych: -cos 2x * (2sin x + 1) = 0. Teraz rozwiąż 2 podstawowe równania trygonometryczne: cos 2x = 0 i (2sin x + 1) = 0.
     • B. Podejście 2.
   • Konwertuje równanie trygonometryczne na równanie trygonometryczne z tylko jedną unikalną funkcją trygonometryczną jako zmienną. Istnieje kilka wskazówek, jak wybrać odpowiednią zmienną. Typowe zmienne to: sin x = t; cos x = t; cos 2x = t, tan x = t i tan (x / 2) = t.
   • Przykład 9. Rozwiąż: 3sin ^ 2 x - 2cos ^ 2 x = 4sin x + 7 (0 x 2Pi).
   • Rozwiązanie. W równaniu zamień (cos ^ 2x) na (1 - sin ^ 2x) i uprość równanie:
   • 3sin ^ 2 x - 2 + 2sin ^ 2 x - 4sin x - 7 = 0. Teraz użyj sin x = t. Równanie wygląda następująco: 5t ^ 2 - 4t - 9 = 0. To jest równanie kwadratowe z 2 pierwiastkami: t1 = -1 it2 = 9/5. Możemy odrzucić drugie t2, ponieważ> 1. Teraz oblicz: t = sin = -1 -> x = 3Pi / 2.
   • Przykład 10. Rozwiąż: tan x + 2 tan ^ 2 x = łóżeczko x + 2.
   • Rozwiązanie. Użyj tan x = t. Zamień podane równanie na równanie, w którym zmienną t jest: (2t + 1) (t ^ 2 - 1) = 0. Znajdź t z tego iloczynu, a następnie rozwiąż standardowe równanie trygonometryczne tg x = t dla x.
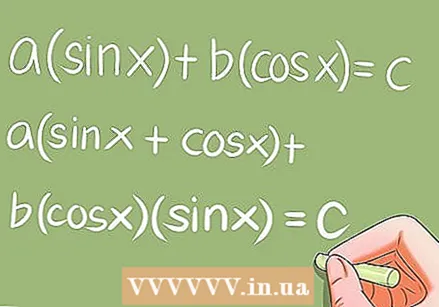7. Rozwiąż specjalne równania trygonometryczne.
   • Istnieje kilka specjalnych równań trygonometrycznych, które wymagają pewnych konkretnych konwersji. Przykłady:
   • a * sin x + b * cos x = c; a (sin x + cos x) + b * cos x * sin x = c;
   • a * sin ^ 2 x + b * sin x * cos x + c * cos ^ 2 x = 0
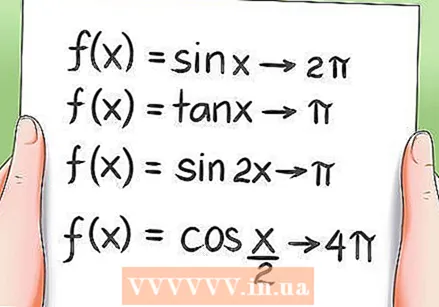8. Poznaj okresowe właściwości funkcji trygonometrycznych.
   • Wszystkie funkcje trygonometryczne są okresowe, co oznacza, że ​​powracają do tej samej wartości po obrocie w pewnym okresie. Przykłady:
     • Funkcja f (x) = sin x ma 2Pi jako okres.
     • Funkcja f (x) = tan x ma Pi jako okres.
     • Funkcja f (x) = sin 2x ma Pi jako okres.
     • Funkcja f (x) = cos (x / 2) ma 4Pi jako okres.
   • Jeśli okres jest określony w ćwiczeniach / teście, wystarczy znaleźć krzywą (-y) x w tym okresie.
   • UWAGA: Rozwiązywanie równań trygonometrycznych jest trudne i często prowadzi do błędów i pomyłek. Dlatego odpowiedzi należy dokładnie sprawdzić. Po rozwiązaniu możesz sprawdzić odpowiedzi za pomocą kalkulatora graficznego, aby uzyskać bezpośrednią reprezentację danego równania trygonometrycznego R (x) = 0. Odpowiedzi (jako pierwiastek kwadratowy) podawane są w miejscach dziesiętnych. Na przykład Pi ma wartość 3,14