Zawartość

• Kroki
• Metoda 1 z 4: Znajdowanie zestawu wartości funkcji za pomocą formuły
• Metoda 2 z 4: Znajdowanie zestawu wartości funkcji na wykresie
• Metoda 3 z 4: Znajdowanie zakresu zbioru współrzędnych
• Metoda 4 z 4: Znajdowanie zakresu w problemach
• Porady

Zbiór wartości (zakres wartości) funkcji to wszystkie wartości, które funkcja przyjmuje w swoim zakresie definicji. Innymi słowy, są to wartości y, które otrzymujesz, gdy podstawisz wszystkie możliwe wartości x. Wszystkie możliwe wartości x i nazywane są dziedziną funkcji. Wykonaj poniższe czynności, aby znaleźć zestaw wartości dla funkcji.

Kroki

Metoda 1 z 4: Znajdowanie zestawu wartości funkcji za pomocą formuły

1. 1 Zapisz funkcję. Na przykład: f (x) = 3x + 6x -2... Wstawiając x do równania, możemy znaleźć wartość y. Jest to funkcja kwadratowa, a jej wykres to parabola.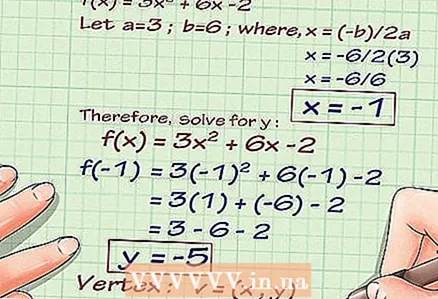
2. 2 Znajdź wierzchołek paraboli. Jeśli otrzymasz funkcję liniową lub dowolną inną funkcję ze zmienną nieparzystego stopnia, na przykład f (x) = 6x + 2x + 7, pomiń ten krok.Ale jeśli masz funkcję kwadratową lub dowolną inną ze zmienną x o parzystej potędze, musisz znaleźć wierzchołek wykresu tej funkcji. Aby to zrobić, użyj wzoru x =-b / 2a... W funkcji 3x + 6x -2 a = 3, b = 6, c = -2. Obliczamy: x = -6 / (2 * 3) = -1.
   • Teraz podłącz x = -1 do funkcji, aby znaleźć y. f (-1) = 3 * (- 1) + 6 * (- 1) -2 = 3 - 6 -2 = -5.
   • Współrzędne wierzchołka paraboli (-1, -5). Narysuj go na płaszczyźnie współrzędnych. Punkt leży w trzeciej ćwiartce płaszczyzny współrzędnych.
3. 3 Znajdź jeszcze kilka punktów na wykresie. Aby to zrobić, wstaw do funkcji kilka innych wartości x. Ponieważ wyraz x jest dodatni, parabola będzie skierowana w górę. Jako siatka bezpieczeństwa podstawiamy kilka wartości x do funkcji, aby dowiedzieć się, jakie wartości y dają.
   • f (-2) = 3 (-2) + 6 (-2) -2 = -2. pierwszy punkt na paraboli (-2, -2)
   • f (0) = 3 (0) + 6 (0) -2 = -2. Drugi punkt na paraboli (0, -2)
   • f (1) = 3 (1) + 6 (1) -2 = 7. Trzeci punkt na paraboli (1, 7).
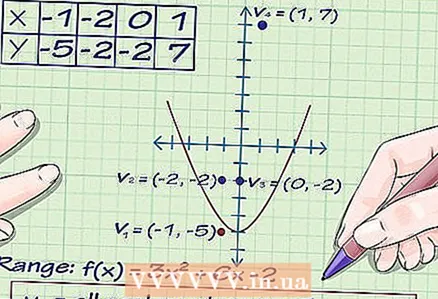4. 4 Znajdź różne wartości funkcji na wykresie. Znajdź najmniejszą wartość y na wykresie. To jest wierzchołek paraboli, gdzie y = -5. Ponieważ parabola leży nad wierzchołkiem, zbiór wartości funkcji r ≥ -5.

Metoda 2 z 4: Znajdowanie zestawu wartości funkcji na wykresie

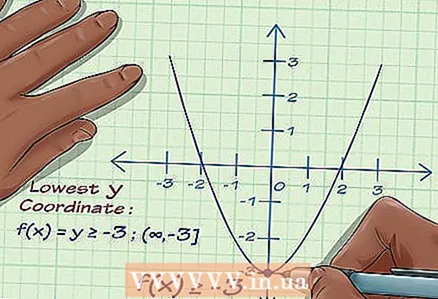1. 1 Znajdź minimum funkcji. Oblicz najmniejszą wartość dla y. Powiedzmy, że minimum funkcji to y = -3. Wartość ta może być coraz mniejsza, aż do nieskończoności, tak aby minimum funkcji nie miało określonego punktu minimum.
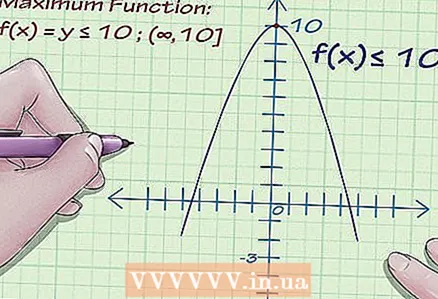2. 2 Znajdź maksymalną funkcję. Załóżmy, że maksimum funkcji y = 10. Podobnie jak w przypadku minimum, maksimum funkcji nie ma określonego punktu maksymalnego.
3. 3 Zapisz różne znaczenia. Zatem zakres wartości funkcji mieści się w zakresie od -3 do +10. Zapisz zbiór wartości funkcji jako: -3 ≤ f (x) ≤ 10
   • Ale na przykład minimum funkcji to y = -3, a maksimum to nieskończoność (wykres funkcji rośnie w nieskończoność). Następnie zestaw wartości funkcji: f (x) ≥ -3.
   • Natomiast jeśli maksimum funkcji y = 10, a minimum to nieskończoność (wykres funkcji spada w nieskończoność), to zbiór wartości funkcji to: f (x) ≤ 10.

Metoda 3 z 4: Znajdowanie zakresu zbioru współrzędnych

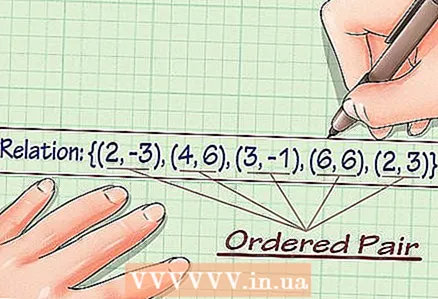1. 1 Zapisz zestaw współrzędnych. Z zestawu współrzędnych można określić jego zakres wartości oraz zakres definicji. Załóżmy, że podano zbiór współrzędnych: {(2, -3), (4, 6), (3, -1), (6, 6), (2, 3)}.
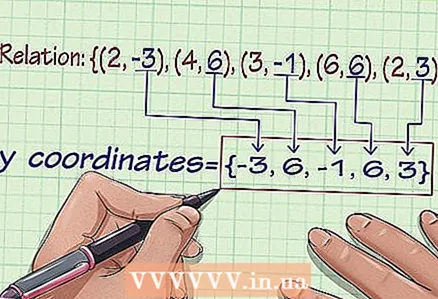2. 2 Wymień wartości y. Aby znaleźć zakres zbioru, po prostu wypisz wszystkie wartości y: {-3, 6, -1, 6, 3}.
3. 3 Usuń wszystkie zduplikowane wartości dla y. W naszym przykładzie usuń „6”: {-3, -1, 6, 3}.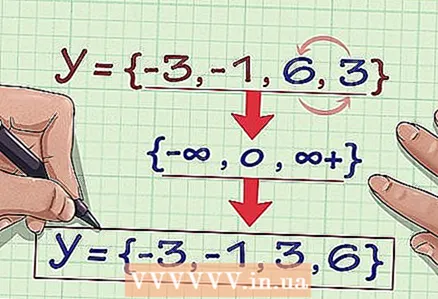
4. 4 Zapisz zakres w porządku rosnącym. Zakres wartości zbioru współrzędnych {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)} będzie wynosił {-3, -1, 3, 6}.
5. 5 Upewnij się, że dla funkcji podano zestaw współrzędnych. Aby tak się stało, dla każdej wartości x musi przypadać jedna wartość y. Na przykład zbiór współrzędnych {(2, 3) (2, 4) (6, 9)} nie jest podany dla funkcji, ponieważ jedna wartość x = 2 odpowiada dwóm różnym wartościom y: y = 3 i y = 4.

Metoda 4 z 4: Znajdowanie zakresu w problemach

1. 1 Przeczytaj problem. „Olga sprzedaje bilety do teatru po 500 rubli za bilet. Całkowity dochód ze sprzedanych biletów jest funkcją liczby sprzedanych biletów. Jaki jest zasięg tej funkcji?”
2. 2 Napisz zadanie jako funkcję. W tym przypadku m to łączne wpływy ze sprzedanych biletów, oraz T - liczba sprzedanych biletów. Ponieważ jeden bilet kosztuje 500 rubli, należy pomnożyć liczbę sprzedanych biletów przez 500, aby obliczyć wpływy. Tak więc funkcję można zapisać jako M(t) = 500t.
   • Na przykład, jeśli sprzedaje 2 bilety, musisz pomnożyć 2 przez 500 - w rezultacie otrzymujemy 1000 rubli, wpływy ze sprzedanych biletów.
3. 3 Znajdź zakres. Aby znaleźć zakres, musisz najpierw znaleźć zakres. To są wszystkie możliwe wartości t. W naszym przykładzie Olga może sprzedać 0 lub więcej biletów - nie może sprzedać ujemnej liczby biletów. Ponieważ nie znamy liczby miejsc w teatrze, można przypuszczać, że teoretycznie mogłaby sprzedać nieskończoną liczbę biletów. I może sprzedawać tylko całe bilety (nie może sprzedać np. 1/2 biletu). Zatem dziedzina funkcji T = dowolna nieujemna liczba całkowita.
4. 4 Znajdź zakres. To możliwa kwota, jaką Olga pomoże ze sprzedaży biletów.Jeśli wiesz, że dziedziną funkcji jest dowolna nieujemna liczba całkowita, a funkcja to: M(t) = 5t, możesz znaleźć wpływy, podstawiając dowolną nieujemną liczbę całkowitą do funkcji (zamiast t). Na przykład, jeśli sprzedaje 5 biletów, to M (5) = 5 * 500 = 2500 rubli. Jeśli sprzeda 100 biletów, to M (100) = 500 x 100 = 50 000 rubli. Zatem zakres wartości funkcji wynosi wszelkie nieujemne liczby całkowite podzielne przez pięćset.
   • Oznacza to, że każda nieujemna liczba całkowita, która jest podzielna przez 500, jest wartością y (przychodów) naszej funkcji.

Porady

• W bardziej skomplikowanych przypadkach lepiej najpierw narysować wykres przy użyciu zakresu definicji, a dopiero potem znaleźć zakres.
• Sprawdź, czy możesz znaleźć funkcję odwrotną. Dziedzina funkcji odwrotnej jest równa domenie funkcji pierwotnej.
• Sprawdź, czy funkcja jest powtarzalna. Każda funkcja, która powtarza się wzdłuż osi x, będzie miała ten sam zakres dla całej funkcji. Na przykład zakres dla f (x) = sin (x) wyniesie -1 do 1.