Zawartość

• Kroki
• Metoda 1 z 3: Część 1: Określanie punktu przegięcia
• Metoda 2 z 3: Obliczanie pochodnych funkcji
• Metoda 3 z 3: Część 3: Znajdź punkt przegięcia
• Porady

W rachunku różniczkowym punkt przegięcia to punkt na krzywej, w którym jego krzywizna zmienia znak (z plus na minus lub z minus na plus). Ta koncepcja jest używana w inżynierii mechanicznej, ekonomii i statystyce do identyfikacji znaczących zmian danych.

Kroki

Metoda 1 z 3: Część 1: Określanie punktu przegięcia

1. 1 Definicja funkcji wklęsłej. Środek dowolnego akordu (odcinka łączącego dwa punkty) wykresu funkcji wklęsłej leży albo pod wykresem, albo na nim.
2. 2 Definicja funkcji wypukłej. Środek dowolnego akordu (odcinka łączącego dwa punkty) wykresu funkcji wypukłej leży albo nad wykresem, albo na nim.
3. 3 Wyznaczanie pierwiastków funkcji. Korzeń funkcji jest wartością zmiennej „x”, przy której y = 0.
   • Podczas wykreślania funkcji pierwiastki to punkty, w których wykres przecina oś x.

Metoda 2 z 3: Obliczanie pochodnych funkcji

1. 1 Znajdź pierwszą pochodną funkcji. Spójrz na zasady różnicowania w podręczniku; musisz nauczyć się brać pierwsze pochodne, a dopiero potem przejść do bardziej złożonych obliczeń. Pierwsze pochodne są oznaczone f '(x). Dla wyrażeń postaci ax ^ p + bx ^ (p − 1) + cx + d, pierwsza pochodna to: apx ^ (p − 1) + b (p - 1) x ^ (p − 2) + c.
   • Na przykład znajdź punkty przegięcia funkcji f (x) = x ^ 3 + 2x -1. Pierwsza pochodna tej funkcji to:
     
     f ′ (x) = (x ^ 3 + 2x - 1) ′ = (x ^ 3) ′ + (2x) ′ - (1) ′ = 3x ^ 2 + 2 + 0 = 3x2 + 2
2. 2 Znajdź drugą pochodną funkcji. Druga pochodna jest pochodną pierwszej pochodnej funkcji pierwotnej. Druga pochodna jest oznaczona jako f ′ ′ (x).
   • W powyższym przykładzie druga pochodna to:
     
     f ′ ′ (x) = (3x2 + 2) ′ = 2 × 3 × x + 0 = 6x
3. 3 Ustaw drugą pochodną na zero i rozwiąż otrzymane równanie. Wynikiem będzie oczekiwany punkt przegięcia.
   • W powyższym przykładzie Twoje obliczenia wyglądają tak:
     
     f ′ ′ (x) = 0
     6x = 0
     x = 0
4. 4 Znajdź trzecią pochodną funkcji. Aby sprawdzić, czy wynik jest faktycznie punktem przegięcia, znajdź trzecią pochodną, ​​która jest pochodną drugiej pochodnej funkcji pierwotnej. Trzecia pochodna jest oznaczona jako f ′ ′ ′ (x).
   • W powyższym przykładzie trzecia pochodna to:
     
     f ′ ′ ′ (x) = (6x) ′ = 6

Metoda 3 z 3: Część 3: Znajdź punkt przegięcia

1. 1 Sprawdź trzecią pochodną. Standardową zasadą szacowania punktu przegięcia jest to, że jeśli trzecia pochodna nie jest równa zero (czyli f ′ ′ ′ (x) ≠ 0), to punkt przegięcia jest prawdziwym punktem przegięcia. Sprawdź trzecią pochodną; jeśli nie jest zerem, to znalazłeś prawdziwy punkt przegięcia.
   • W powyższym przykładzie trzecia pochodna to 6, a nie 0.Więc znalazłeś prawdziwy punkt przegięcia.
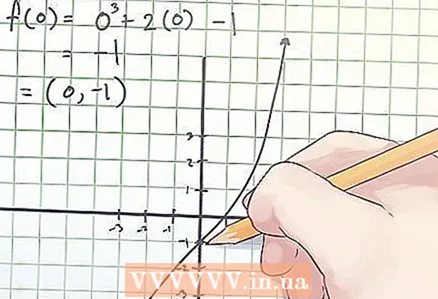2. 2 Znajdź współrzędne punktu przegięcia. Współrzędne punktu przegięcia oznaczono jako (x, f (x)), gdzie x jest wartością zmiennej niezależnej „x” w punkcie przegięcia, f (x) jest wartością zmiennej zależnej „y” w punkcie przegięcia punkt.
   • W powyższym przykładzie, przyrównując drugą pochodną do zera, okazało się, że x = 0. Aby określić współrzędne punktu przegięcia, znajdź f (0). Twoje obliczenia wyglądają tak:
     
     f (0) = 0 ^ 3 + 2 × 0−1 = −1.
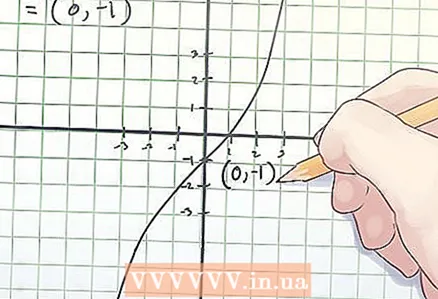3. 3 Zapisz współrzędne punktu przegięcia. Współrzędne punktu przegięcia to znalezione wartości x i f (x).
   • W powyższym przykładzie punkt przegięcia znajduje się na współrzędnych (0, -1).

Porady

• Pierwsza pochodna wyrazu wolnego (liczba pierwsza) to zawsze zero.