Zawartość

• Kroki

Równanie trygonometryczne zawiera jedną lub więcej funkcji trygonometrycznych zmiennej „x” (lub dowolnej innej zmiennej). Rozwiązanie równania trygonometrycznego polega na znalezieniu takiej wartości „x”, która spełnia funkcję (funkcje) i równanie jako całość.

• Rozwiązania równań trygonometrycznych są wyrażone w stopniach lub radianach. Przykłady:

x = π / 3; x = 5π/6; x = 3π/2; x = 45 stopni; x = 37,12 stopnia; x = 178,37 stopni.

• Uwaga: wartości funkcji trygonometrycznych z kątów wyrażonych w radianach i z kątów wyrażonych w stopniach są równe. Okrąg trygonometryczny o promieniu równym jeden służy do opisu funkcji trygonometrycznych, a także do sprawdzenia poprawności rozwiązania podstawowych równań i nierówności trygonometrycznych.
• Przykłady równań trygonometrycznych:
  • grzech x + grzech 2x = 1/2; tgx + ctgx = 1,732;
  • cos 3x + sin 2x = cos x; 2sin 2x + cos x = 1.

1. Okrąg trygonometryczny o promieniu równym jeden (okrąg jednostkowy).
   • Jest to okrąg o promieniu równym jeden i środku w punkcie O. Okrąg jednostkowy opisuje 4 podstawowe funkcje trygonometryczne zmiennej „x”, gdzie „x” jest kątem mierzonym od kierunku dodatniego osi X w kierunku przeciwnym do ruchu wskazówek zegara.
   • Jeśli „x” jest jakimś kątem na okręgu jednostkowym, to:
   • Oś pozioma OAx definiuje funkcję F (x) = cos x.
   • Oś pionowa OBY definiuje funkcję F (x) = sin x.
   • Oś pionowa AT definiuje funkcję F (x) = tan x.
   • Oś pozioma BU definiuje funkcję F (x) = ctg x.

• Koło jednostkowe służy również do rozwiązywania podstawowych równań trygonometrycznych i nierówności (rozważane są na nim różne pozycje „x”).

Kroki

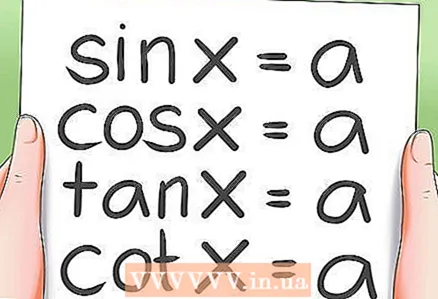1. 1 Pojęcie rozwiązywania równań trygonometrycznych.
   • Aby rozwiązać równanie trygonometryczne, przekształć je w jedno lub więcej podstawowych równań trygonometrycznych. Rozwiązanie równania trygonometrycznego ostatecznie sprowadza się do rozwiązania czterech podstawowych równań trygonometrycznych.
2. 2 Rozwiązywanie podstawowych równań trygonometrycznych.
   • Istnieją 4 rodzaje podstawowych równań trygonometrycznych:
   • sin x = a; cos x = a
   • tg x = a; ctg x = a
   • Rozwiązywanie podstawowych równań trygonometrycznych polega na spojrzeniu na różne pozycje x na okręgu jednostkowym i użyciu tabeli konwersji (lub kalkulatora).
   • Przykład 1.sin x = 0,866. Korzystając z tabeli przeliczeniowej (lub kalkulatora), otrzymujesz odpowiedź: x = π / 3. Koło jednostkowe daje inną odpowiedź: 2π / 3. Pamiętaj: wszystkie funkcje trygonometryczne są okresowe, to znaczy ich wartości się powtarzają. Na przykład okresowość sin x i cos x wynosi 2πn, a okresowość tg x i ctg x wynosi πn. Dlatego odpowiedź jest napisana w następujący sposób:
   • x1 = π/3 + 2πn; x2 = 2π / 3 + 2πn.
   • Przykład 2.cos x = -1/2. Korzystając z tabeli przeliczeniowej (lub kalkulatora), otrzymujesz odpowiedź: x = 2π / 3. Koło jednostkowe daje inną odpowiedź: -2π / 3.
   • x1 = 2π/3 + 2π; x2 = -2π/3 + 2π.
   • Przykład 3.tg (x - π / 4) = 0.
   • Odpowiedź: x = π / 4 + πn.
   • Przykład 4. ctg 2x = 1,732.
   • Odpowiedź: x = π/12 + πn.
3. 3 Transformacje stosowane do rozwiązywania równań trygonometrycznych.
   • Do przekształcenia równań trygonometrycznych stosuje się przekształcenia algebraiczne (faktoryzacja, redukcja wyrazów jednorodnych itp.) oraz tożsamości trygonometryczne.
   • Przykład 5. Korzystając z tożsamości trygonometrycznych, równanie sin x + sin 2x + sin 3x = 0 jest przekształcane w równanie 4cos x * sin (3x / 2) * cos (x / 2) = 0. Dlatego musisz rozwiązać następujące podstawowe równania trygonometryczne: cos x = 0; grzech (3x / 2) = 0; cos (x / 2) = 0.
     
     
4. 4 Znajdowanie kątów ze znanych wartości funkcji.
   • Zanim poznasz metody rozwiązywania równań trygonometrycznych, musisz nauczyć się znajdować kąty ze znanych wartości funkcji. Można to zrobić za pomocą tabeli przeliczeniowej lub kalkulatora.
   • Przykład: cos x = 0,732. Kalkulator poda odpowiedź x = 42,95 stopnia. Okrąg jednostkowy da dodatkowe kąty, których cosinus również wynosi 0,732.
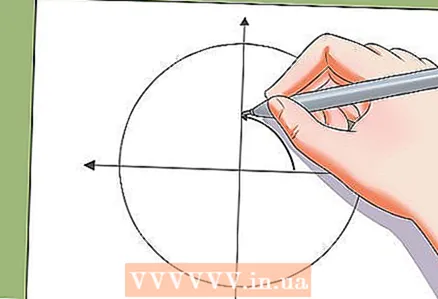5. 5 Odłóż rozwiązanie na bok na okręgu jednostek.
   • Możesz odroczyć rozwiązania równania trygonometrycznego na okręgu jednostkowym. Rozwiązaniami równania trygonometrycznego na okręgu jednostkowym są wierzchołki wielokąta foremnego.
   • Przykład: Rozwiązania x = π / 3 + πn / 2 na okręgu jednostkowym są wierzchołkami kwadratu.
   • Przykład: Rozwiązania x = π / 4 + πn / 3 na okręgu jednostkowym reprezentują wierzchołki sześciokąta foremnego.
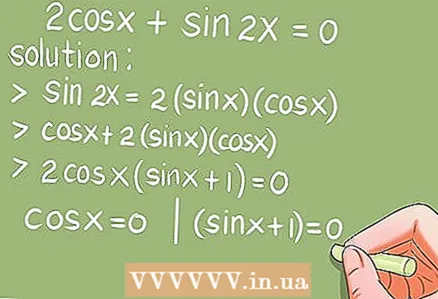6. 6 Metody rozwiązywania równań trygonometrycznych.
   • Jeśli dane równanie trygonometryczne zawiera tylko jedną funkcję trygonologiczną, rozwiąż to równanie jako podstawowe równanie trygonometryczne.Jeżeli dane równanie zawiera dwie lub więcej funkcji trygonometrycznych, to istnieją 2 metody rozwiązania takiego równania (w zależności od możliwości jego przekształcenia).
     • Metoda 1.
   • Przekształć to równanie w równanie o postaci: f (x) * g (x) * h (x) = 0, gdzie f (x), g (x), h (x) są podstawowymi równaniami trygonometrycznymi.
     
     
   • Przykład 6.2 cos x + sin 2x = 0. (0 x 2π)
   • Rozwiązanie. Używając formuły podwójnego kąta sin 2x = 2 * sin x * cos x, zastąp sin 2x.
   • 2cos x + 2 * sin x * cos x = 2cos x * (sin x + 1) = 0. Teraz rozwiąż dwa podstawowe równania trygonometryczne: cos x = 0 i (sin x + 1) = 0.
   • Przykład 7.cos x + cos 2x + cos 3x = 0. (0 x 2π)
   • Rozwiązanie: Używając tożsamości trygonometrycznych, przekształć to równanie w równanie postaci: cos 2x (2cos x + 1) = 0. Teraz rozwiąż dwa podstawowe równania trygonometryczne: cos 2x = 0 i (2cos x + 1) = 0.
   • Przykład 8.sin x - sin 3x = cos 2x. (0 x 2π)
   • Rozwiązanie: Używając tożsamości trygonometrycznych, przekształć to równanie w równanie postaci: -cos 2x * (2sin x + 1) = 0. Teraz rozwiąż dwa podstawowe równania trygonometryczne: cos 2x = 0 i (2sin x + 1) = 0.
     • Metoda 2.
   • Przekształć podane równanie trygonometryczne na równanie zawierające tylko jedną funkcję trygonometryczną. Następnie zastąp tę funkcję trygonometryczną jakąś nieznaną, na przykład t (sin x = t; cos x = t; cos 2x = t, tg x = t; tg (x / 2) = t, itd.).
   • Przykład 9.3sin^2x - 2cos^2x = 4sin x + 7 (0 x 2π).
   • Rozwiązanie. W tym równaniu zamień (cos ^ 2 x) na (1 - sin ^ 2 x) (przez identyczność). Przekształcone równanie to:
   • 3sin ^ 2 x - 2 + 2sin ^ 2 x - 4sin x - 7 = 0. Zamień sin x na t. Równanie wygląda teraz tak: 5t^2 - 4t - 9 = 0. Jest to równanie kwadratowe z dwoma pierwiastkami: t1 = -1 i t2 = 9/5. Drugi pierwiastek t2 nie spełnia zakresu wartości funkcji (-1 sin x 1). Teraz zdecyduj: t = sin x = -1; x = 3π / 2.
   • Przykład 10.tg x + 2 tg ^ 2 x = ctg x + 2
   • Rozwiązanie. Zamień tg x na t. Przepisz oryginalne równanie w następujący sposób: (2t + 1) (t ^ 2 - 1) = 0. Teraz znajdź t, a następnie znajdź x dla t = tg x.
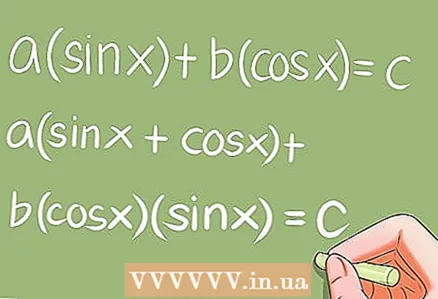7. 7 Specjalne równania trygonometryczne.
   • Istnieje kilka specjalnych równań trygonometrycznych, które wymagają określonych przekształceń. Przykłady:
   • a * sin x + b * cos x = c; a (sin x + cos x) + b * cos x * sin x = c;
   • a * sin ^ 2 x + b * sin x * cos x + c * cos ^ 2 x = 0
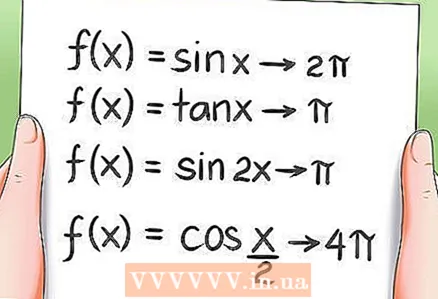8. 8 Okresowość funkcji trygonometrycznych.
   • Jak wspomniano wcześniej, wszystkie funkcje trygonometryczne są okresowe, to znaczy ich wartości powtarzają się po pewnym okresie. Przykłady:
     • Okres funkcji f(x) = sin x wynosi 2π.
     • Okres funkcji f (x) = tan x jest równy π.
     • Okres funkcji f(x) = sin 2x wynosi π.
     • Okres funkcji f (x) = cos (x / 2) wynosi 4π.
   • Jeśli okres jest określony w zadaniu, oblicz wartość „x” w tym okresie.
   • Uwaga: Rozwiązywanie równań trygonometrycznych nie jest łatwym zadaniem i często prowadzi do błędów. Dlatego dokładnie sprawdź swoje odpowiedzi. W tym celu można użyć kalkulatora graficznego, aby wykreślić dane równanie R(x) = 0. W takich przypadkach rozwiązania będą prezentowane jako ułamki dziesiętne (tzn. π jest zastąpione przez 3,14).