Jak rozłożyć liczbę na iloczyn czynników pierwszych?

Wideo: Rozkład liczby na czynniki pierwsze - Matematyka Szkoła Podstawowa i Gimnazjum

Zawartość

Kroki
Część 1 z 2: Znajdowanie czynników pierwszych
Część 2 z 2: Korzystanie z czynników pierwszych
Przykłady zadań
Porady
Ostrzeżenia

Dowolną liczbę naturalną można rozłożyć na iloczyn czynników pierwszych. Jeśli nie lubisz zajmować się dużymi liczbami, takimi jak 5733, naucz się je rozkładać (w tym przypadku 3 x 3 x 7 x 7 x 13). Podobne zadanie często spotyka się w kryptografii, która zajmuje się problemami bezpieczeństwa informacji. Jeśli nie jesteś jeszcze gotowy na zbudowanie własnego bezpiecznego systemu poczty e-mail, naucz się najpierw rozkładać liczby na czynniki.

Kroki

Część 1 z 2: Znajdowanie czynników pierwszych

1 Dowiedz się, czym jest faktoring. Rozkład liczby na iloczyn czynników to proces „dzielenia” jej na mniejsze części.Po pomnożeniu te części lub współczynniki dają pierwotną liczbę.
- Na przykład liczbę 18 można rozłożyć na następujące iloczyny: 1 x 18, 2 x 9 lub 3 x 6.
2 Pamiętaj, jakie są liczby pierwsze. Liczba pierwsza jest podzielna tylko przez dwie liczby bez reszty: przez samą siebie i przez 1. Na przykład liczbę 5 można przedstawić jako iloczyn 5 i 1. Tej liczby nie można rozłożyć na inne czynniki. Celem rozłożenia liczby na czynniki pierwsze jest przedstawienie jej jako iloczynu liczb pierwszych. Jest to szczególnie przydatne w przypadku ułamków, ponieważ pozwala je porównywać i upraszczać.
3 Zacznij od oryginalnego numeru. Wybierz liczbę złożoną większą niż 3. Nie ma sensu brać liczby pierwszej, ponieważ jest ona podzielna tylko przez siebie i jeden.
- Przykład: Rozłóżmy liczbę 24 na iloczyn liczb pierwszych.
4 Podzielmy tę liczbę na iloczyn dwóch czynników. Znajdź dwie mniejsze liczby, których iloczyn jest równy oryginalnej liczbie. Można użyć dowolnego współczynnika, ale łatwiej jest wziąć liczby pierwsze. Dobrym sposobem jest próba podzielenia pierwotnej liczby najpierw przez 2, potem przez 3, potem przez 5 i sprawdzenie, którą z tych liczb pierwszych dzieli bez reszty.
- Przykład: Jeśli nie znasz współczynników 24, spróbuj podzielić je przez małe liczby pierwsze. Więc przekonasz się, że podana liczba jest podzielna przez 2: 24 = 2x12... To dobry początek.
- Ponieważ 2 jest liczbą pierwszą, dobrze jest używać jej przy rozkładaniu liczb parzystych.
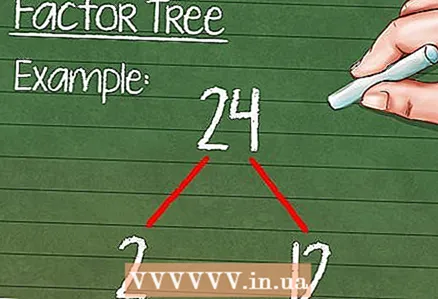5 Zacznij budować drzewko mnożnika. Ta prosta procedura pomoże Ci rozłożyć liczbę. Na początek narysuj dwie „gałęzie” od oryginalnej liczby. Na końcu każdej gałęzi zapisz znalezione czynniki.
- Przykład:
- 24
- /
- 2 12
6 Rozłóż następny rząd liczb na czynniki. Spójrz na dwie nowe liczby (drugi rząd drzewa mnożników). Czy to obie liczby pierwsze? Jeśli jeden z nich nie jest prosty, podziel go również na dwa czynniki. Zrób jeszcze dwie gałęzie i napisz dwa nowe czynniki w trzecim wierszu drzewa.
- Przykład: 12 nie jest liczbą pierwszą, więc należy ją rozłożyć na czynniki. Użyj rozkładu 12 = 2 x 6 i zapisz go w trzecim wierszu drzewa:
- 24
- /
- 2 12
- /
- 2x6
7 Idź dalej w dół drzewa. Jeśli jeden z nowych czynników okaże się liczbą pierwszą, wyciągnij z niej jedną „gałąź” i na jej końcu wpisz tę samą liczbę. Liczb pierwszych nie można rozszerzyć na mniejsze czynniki, więc po prostu przesuń je w dół o jeden poziom.
- Przykład: 2 to liczba pierwsza. Po prostu przesuń 2 z drugiej do trzeciej linii:
- 24
- /
- 2 12
- / /
- 2 2 6
8 Kontynuuj rozkładanie liczb na czynniki, aż pozostaną tylko liczby pierwsze. Sprawdź każdą nową linię drzewa. Jeśli przynajmniej jeden z nowych czynników nie jest liczbą pierwszą, rozłóż go na czynniki i napisz nowy wiersz. W końcu pozostaniesz tylko z liczbami pierwszymi.
- Przykład: 6 nie jest liczbą pierwszą, więc należy ją również rozłożyć na czynniki. Jednocześnie 2 jest liczbą pierwszą i przenosimy te dwie dwójki na wyższy poziom:
- 24
- /
- 2 12
- / /
- 2 2 6
- / / /
- 2 2 2 3
9 Napisz ostatnią linię jako iloczyn czynników pierwszych. W końcu pozostaniesz tylko z liczbami pierwszymi. Kiedy tak się dzieje, rozkład na czynniki pierwsze jest zakończony. Ostatnia linia to zbiór liczb pierwszych, których iloczyn daje pierwotną liczbę.
- Sprawdź swoją odpowiedź: pomnóż liczby w ostatniej linii. Wynik powinien być oryginalną liczbą.
- Przykład: Ostatni wiersz drzewa czynników zawiera liczby 2 i 3. Obie te liczby są liczbami pierwszymi, więc rozkład jest kompletny. Zatem pierwsza faktoryzacja liczby 24 ma następującą postać: 24 = 2 x 2 x 2 x 3.
- Kolejność czynników nie ma znaczenia. Rozkład można również zapisać jako 2 x 3 x 2 x 2.
10 Uprość odpowiedź, używając notacji wykładniczej, jeśli chcesz. Jeśli znasz potęgowanie liczb, możesz napisać odpowiedź w prostszej formie.Pamiętaj, że podstawa jest napisana na dole, a liczba w indeksie górnym wskazuje, ile razy ta podstawa powinna zostać pomnożona przez samą siebie.
- Przykład: ile razy liczba 2 występuje w znalezionej dekompozycji 2 x 2 x 2 x 3? Trzy razy, więc wyrażenie 2 x 2 x 2 można zapisać jako 2. W notacji uproszczonej otrzymujemy 2x3.

Część 2 z 2: Korzystanie z czynników pierwszych

1 Znajdź największy wspólny dzielnik dwóch liczb. Największy wspólny dzielnik (NWD) dwóch liczb to maksymalna liczba, przez którą obie liczby są podzielne bez reszty. Poniższy przykład pokazuje, jak użyć rozkładu na czynniki pierwsze, aby znaleźć największy wspólny dzielnik 30 i 36.
- Rozłóżmy obie liczby na czynniki pierwsze. Dla 30 faktoryzacja wynosi 2 x 3 x 5. Liczba 36 jest rozkładana na czynniki pierwsze w następujący sposób: 2 x 2 x 3 x 3.
- Znajdźmy liczbę występującą w obu rozszerzeniach. Przekreślmy ten numer na obu listach i wpiszmy go w nowej linii. Na przykład 2 występuje w dwóch rozszerzeniach, więc piszemy 2 na nowej linii. Potem mamy 30 = 2 x 3 x 5 i 36 = 2 x 2 x 3 x 3.
- Powtarzaj ten krok, aż w rozszerzeniach nie będą już żadnych wspólnych czynników. Obie listy zawierają również cyfrę 3, więc w nowej linii możesz pisać 2 oraz 3... Następnie ponownie porównaj rozszerzenia: 30 = ~~2x3~~ x 5 i 36 = 2 x 2 x 3 x 3. Jak widać, nie ma w nich żadnych wspólnych czynników.
- Aby znaleźć największy wspólny czynnik, znajdź iloczyn wszystkich wspólnych czynników. W naszym przykładzie są to 2 i 3, więc gcd to 2 x 3 = 6... Jest to największa liczba, która równo dzieli liczby 30 i 36.
2 Za pomocą GCD możesz uprościć ułamki. Jeśli podejrzewasz, że ułamek można anulować, użyj największego wspólnego dzielnika. Znajdź NWD licznika i mianownika, korzystając z powyższej procedury. Następnie podziel licznik i mianownik ułamka przez tę liczbę. W rezultacie otrzymujesz ten sam ułamek w prostszej formie.
- Na przykład uprośćmy ułamek /₃₆... Jak powiedzieliśmy powyżej, dla 30 i 36 NWD wynosi 6, więc dzielimy licznik i mianownik przez 6:
- 30 ÷ 6 = 5
- 36 ÷ 6 = 6
- /₃₆ = /₆
3 Znajdź najmniejszą wspólną wielokrotność dwóch liczb. Najmniejsza wspólna wielokrotność (LCM) dwóch liczb to najmniejsza liczba podzielna przez obie liczby. Na przykład LCM z 2 i 3 to 6, ponieważ jest to najmniejsza liczba podzielna przez 2 i 3. Poniżej znajduje się przykład znajdowania LCM przy użyciu faktoryzacji liczb pierwszych:
- Zacznijmy od dwóch rozkładów liczb pierwszych. Na przykład dla 126 rozkład na czynniki można zapisać jako 2 x 3 x 3 x 7. Liczbę 84 można rozłożyć na czynniki pierwsze jako 2 x 2 x 3 x 7.
- Porównajmy ile razy każdy czynnik występuje w rozszerzeniach. Wybierz listę, na której mnożnik wystąpi maksymalną liczbę razy, i zakreśl to miejsce. Na przykład liczba 2 pojawia się raz w rozszerzeniu dla 126 i dwukrotnie na liście dla 84, więc należy zakreślić 2x2 na drugiej liście czynników.
- Powtórz ten krok dla każdego mnożnika. Na przykład 3 jest bardziej powszechne w pierwszym rozszerzeniu, więc powinieneś w nim zakreślić 3x3... Liczba 7 pojawia się raz na obu listach, więc zakreślamy 7 (nie ma znaczenia na której liście, jeśli dany czynnik występuje na obu listach tyle samo razy).
- Aby znaleźć LCM, pomnóż wszystkie zakreślone liczby. W naszym przykładzie najmniejsza wspólna wielokrotność 126 i 84 to 2 x 2 x 3 x 3 x 7 = 252... Jest to najmniejsza liczba podzielna przez 126 i 84 bez reszty.
4 Użyj LCM do dodawania frakcji. Przy dodawaniu dwóch ułamków konieczne jest doprowadzenie ich do wspólnego mianownika. Aby to zrobić, znajdź LCM dwóch mianowników. Następnie pomnóż licznik i mianownik każdego ułamka przez taką liczbę, aby mianowniki ułamków były równe LCM. Następnie możesz dodać ułamki.
- Na przykład musisz znaleźć kwotę /₆ + /₂₁.
- Używając powyższej metody, możesz znaleźć LCM dla 6 i 21. Jest to 42.
- Przekształcamy ułamek /₆ aby jego mianownik wynosił 42. Aby to zrobić, musisz podzielić 42 przez 6: 42 ÷ 6 = 7. Teraz pomnóż licznik i mianownik ułamka przez 7: /₆ x /₇ = /₄₂.
- Aby sprowadzić drugi ułamek do mianownika 42, podziel 42 przez 21: 42 ÷ 21 = 2. Pomnóż licznik i mianownik ułamka przez 2: /₂₁ x /₂ = /₄₂.
- Po zredukowaniu ułamków do tego samego mianownika można je łatwo dodać: /₄₂ + /₄₂ = /₄₂.

Przykłady zadań

Spróbuj sam rozwiązać poniższe problemy.Jeśli uważasz, że otrzymałeś poprawną odpowiedź, zaznacz myszą miejsce po dwukropku w opisie problemu. Te ostatnie zadania są najtrudniejsze.
Znajdź rozkład na czynniki pierwsze dla 16: 2 x 2 x 2 x 2
Napisz odpowiedź w formie wykładniczej: 2
Znajdź pierwszą faktoryzację 45: 3 x 3 x 5
Napisz odpowiedź w formie wykładniczej: 3 x 5
Znajdź rozkład na czynniki pierwsze dla 34: 2 x 17
Znajdź pierwszą faktoryzację liczby 154: 2 x 7 x 11
Znajdź rozkład na czynniki pierwsze dla 8 i 40, a następnie określ ich największy wspólny dzielnik: rozkład na czynniki pierwsze 8 to 2 x 2 x 2 x 2; pierwsza faktoryzacja 40 to 2 x 2 x 2 x 5; NWD dwóch liczb 2 x 2 x 2 = 6.
Znajdź rozkład na czynniki pierwsze dla 18 i 52 i znajdź ich najmniejszą wspólną wielokrotność: Rozkład na czynniki pierwsze 18 to 2 x 3 x 3; faktoryzacja pierwsza 52 wynosi 2 x 2 x 13; LCM dwóch liczb to 2 x 2 x 3 x 3 x 13 = 468.

Porady

Każda liczba ma unikalną cechę faktoryzacji. Nie ma znaczenia, jak znajdziesz to rozszerzenie, powinieneś otrzymać tę samą odpowiedź. Nazywa się to podstawowym twierdzeniem arytmetyki.
Zamiast za każdym razem przepisywać liczby pierwsze w nowym wierszu drzewa czynnikowego, możesz pozostawić je na miejscu i po prostu je zakreślić. Pod koniec rozszerzenia będzie zawierał wszystkie zakreślone w kółku czynniki pierwsze.
Zawsze sprawdzaj otrzymaną odpowiedź. Możesz popełnić błąd i tego nie zauważyć.
Przygotuj się na trudne misje. Jeśli zostaniesz poproszony o znalezienie rozkładu na czynniki pierwsze liczby pierwszej, nie ma potrzeby wykonywania żadnych obliczeń. Na przykład dla liczby 17 faktoryzacja pierwsza wynosi 17; liczba ta nie może być rozłożona na inne czynniki pierwsze.
Największy wspólny dzielnik i najmniejszą wspólną wielokrotność można znaleźć dla trzech lub więcej liczb.